Super Sudoku '81

Super Sudoku '81 (play it now!) is my attempt to combine a couple of hobbies - ZX81 preservation/programming and Sudoku. I had already spent some time writing a Sudoku solving program in Java, and decided to complete it on the ZX81. The overall process took a couple of months, starting from the working Java program.

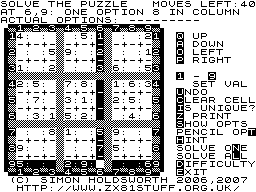
Here's a screenshot of the program in action, solving a 9x9 puzzle.

Program Features

I decided to be quite ambitious and write a fully functional Sudoku program, with both the 9x9 and 6x6 puzzle variants. The program includes the ability to generate puzzles, check for solutions, provide hints, as well as include full instructions:

• Instructions
  Included are 7 full screen pages of instructions, explaining how to play the game, use the interface, and interpret the hint messages that the program produces.
   
• 9x9 and 6x6 puzzles
  As well as the standard 9x9 puzzle with 3x3 blocks, the program also provides the 6x6 puzzle with 3x2 blocks. I had considered also including an 8x8 variant with the two main diagonals and overlapping 4x2 blocks, but that would require significant restructuring of the code, and would be very difficult to display.
   
• Built-in puzzles
  I've included a small selection of puzzles of a variety of difficulties to get going quickly with the program.
   
• Manual puzzle entry
  Puzzles can be entered from magazines. While entering the puzzle its possible to check whether the puzzle as currently set up has unique solution.
   
• Puzzle generation
  The program can generate a random puzzle, with a range of possible difficulties. Generation of a puzzle takes around 1 minute.
   
• Difficulty rating
  Using the in-built logic rules, the program can estimate the difficulty of a puzzle - based on the sophistication of the rules required to solve the puzzle.
   
• Hints
  The in-built logic allows the program to display a hint as to the next move that the program would take, i.e. the location on the board, the type of move (place a number or remove an option), and the number/option value. Once all logic rules are exhausted, the program resorts to brute force.
   
• Splash screen
  Surprisingly few ZX81 programs make use of the fact that the display file is saved and loaded with the program, meaning that for little extra loading time, a screen can automatically be displayed once the program is loaded, with no additional use of memory from the program iself. Here's the splash screen for the Sudoku program:

  

Challenges

Given the limitations of the ZX81, the challenges in programming this are:

1. Memory
   To get the program logic, messages, display, internal state and instruction text into 16K. To achieve this, run length and dictionary compression is used in the instruction text, and quite a long time was spent optimising the code to extract common functions and trim down the instruction count. In the end the program comes out at around 14K, so there would be room for additional features if I had time to add them.
    
2. Display
   Displaying the sudoku board, options and other information on the ZX81 screen is quite a challenge. I could have used the software high-resolution routines, but that would have left insufficient room for the program logic.
    
3. Speed
   For the hints and board generation, the algorithm needed to be fast enough to be reasonably usable. This means the program has to be written completely in ZX81 machine code. I manually "compiled" the original Java source directly into z80 assembler.

Program logic

The program includes the following logical rules that it uses to provide hints and generate puzzles. The rules are listed in order of complexity:

1. Find a number to place
   a) Identify a cell that has a single option
   b) Identify the only cell in a row, column or block that can contain a given number.
    
2. Check pencilled options
   Checks the user's pencilled options to find if one of the can be removed.
    
3. Find an option to remove
   a) Within a given block, if an option appears only in one row, it can be removed from other cells in that row outside of the block.
   b) as a) for columns instead of rows.
    
   c) Within a given row, if an option appears in only one block, it can be removed from other cells in that block outside of the row.
   d) as c) for columns instead of rows.
    
   e) (closed set; outside) if a set of n cells in a row contain a maximum of n different options, the options can be removed from other cells in that row.
   f) as for e) with columns
   g) as for e) with blocks
    
   h) (X-wing column) If an option appears twice in two rows in the same columns, the option can be removed from other cells in those columns
   i) (X-wing row) If an option appears twice in two columns in the same rows, the option can be removed from other cells in those rows
    
   j) (brute force) Choose a valid option in an empty cell and see if the puzzle can then be solved; if not, choose a different valid option.

I've realised that the "closed set" rules are not complete - there's another closed set rule that removes extra options from a set of n cells that contain at most n options that don't appear elsewhere in the row/column/block.

There are additional rules I'm aware of, and have used when manually solving Sudoku puzzles, for example Y-wings, however I've not had the time/inclination to implement every rule in this program.

Program listing

For anyone interested, I've included the full assembly listing of the program. I use the TASM assembler to assemble this, the output of which is a fully-working ZX81 .P file.

The program itself

Play the game now!.

Download the program as a .P file and as a .TZX file.